The curve that changed the world: The Brachistochrone
- Harsh Bhundiya
- Jul 2, 2022
- 3 min read
Updated: Aug 7, 2022
Roller coasters, skate parks, Olympic skiing, and airplane trajectories. What do these things have in common? All applications of the brachistochrone curve!
In June 1696, Johann Bernoulli (a famous mathematician from the Bernoulli family) posed a problem to other mathematicians of his time: Given two points A and B on a plane, what is the shape of a curve between the points which results in the shortest travel time for a frictionless ball only acted on by gravity?

At first you might think this problem is simplistic: obviously the answer is a straight line between A and B, right? Well turns out it’s not that simple, and the derivation of the answer involves minimizing the time taken to traverse the curve using calculus of variations.
Don’t fret if that wasn’t obvious. When the problem was originally posed, it proved to be a challenge for even the most brilliant mathematicians of the time: Newton, Leibniz, Von Tschirnahus, and L’Hopital. Even Galileo, who had thought about this problem decades earlier, incorrectly guessed that the answer was a circular arc between points A and B.
The correct answer, as derived by Newton, uses calculus to minimize a “functional”, i.e. a function of functions, which represents the time taken to traverse the curve. This functional is given by:
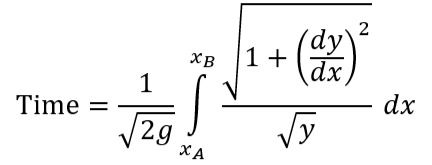
where x(t), y(t) are the parametric coordinates of the curve between points A and B and g is the acceleration due to gravity. This functional is derived using the fact that for a rolling ball, the gravitational potential energy and kinetic energy are equal at all points along the curve. Minimizing this functional, we find parametric equations for x(t), y(t) which define a curve with the minimal travel time between A and B under gravity:
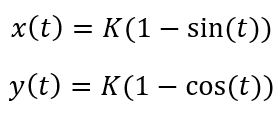
Plotting these functions, we find…you guessed it…the brachistochrone curve (in red below). We clearly see that the brachistochrone curve achieves the fastest time for the ball to roll down from A to B.
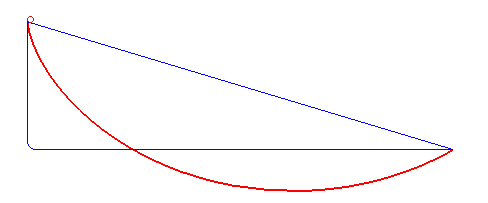
Now you might think this curve is just the result of a mathematical exercise, but in fact the curve has numerous engineering applications which would likely surprise the 17th century mathematicians who discovered it. For instance, the curve is used by roller coaster designers to achieve the fastest speed at the bottom of a track with the least amount of elevation change. It is also useful in sports: skiers use it to plan their trajectory to achieve maximum speed on the slopes. As we see from above, this maximum speed trajectory isn’t simply linear! Brachistochrone curves are also useful for designing half-pipes in skateparks, as they are the ideal shape to get maximum speed at the center of the structure (in reality the shape needs to be tweaked to account for friction).
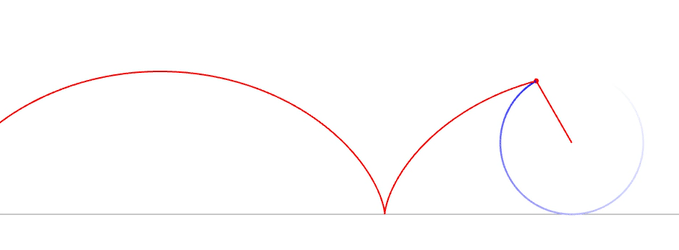
The brachistochrone is also special for another reason: any ball that is placed along the curve will reach the bottom at the same time (under uniform gravity). A direct consequence of this equal-time property is that all balls rolling up and down the brachistochrone have the same frequency. See for yourself:

This remarkable property is unique to a class of curves called “cycloids,” which are formed by tracing out points on the edge of a circle as it rolls along a straight edge. The brachistochrone is one such cycloid, as seen below.
The discovery of the brachistochrone curve did more than just reveal these amazing properties. It led to the development of a whole new branch of mathematics, the calculus of variations, which seeks to find extrema of functionals like above. The work in this area by Euler and Lagrange through the 18th century transformed our understanding of differential equations and calculus. Today, the calculus of variations is used in many branches of engineering, including differential geometry, computational geometry, analytic mechanics, and computational mechanics. For instance, the Euler-Lagrange differential equations, derived using the calculus of variations, are used to find equations of motion, natural frequencies, and natural modes of multi-DOF systems. Another application is in theoretical solutions to buckling of rods, plates, and shells, where the minimized functional is the total potential energy of the system. Yet another application (potentially more familiar) is in calculating geodesics of a surface, which are used to plan the shortest airplane trajectories around the Earth.
So next time you board a plane or see a ball rolling down a hill, remember how a simple question posed more than 300 years ago led to the discovery of an amazing class of curves and forever changed our understanding of calculus.
References/further reading:



Comments