The great inflatable tube dancer
- Harsh Bhundiya
- Jun 4, 2023
- 4 min read
We’ve all seen those inflatable tube dancers – the long tubes with wacky waving arms. But did you know they debuted at the 1996 Olympics as art? And that their mesmerizing dance moves can be explained with shell buckling?
Those wacky waving inflatable tubes are everywhere – car lots, shopping malls, even parties. Besides being an ingenious way to get your attention, they show some pretty cool dance moves, too. But how do they work? And what causes their mesmerizing dance moves?

Let’s start with a bit of history. The invention of the inflatable tube dancer is credited to the Caribbean artist Peter Minshall. In the 1980s, he became known for making large, manned dancing puppets for the Carnival in Trinidad and Tobago. Minshall was featured in a book called Caribbean Festival Arts, and this book somehow reached a man on the steering committee of the Olympics. Seeing the opportunity for collaboration, Minshall was commissioned to help create an unforgettable opening for the 1996 Summer Olympics. So, using his knowledge of puppets and with the help of an engineer, Minshall created the first-ever inflatable tube dancers: two-legged, 60 ft dancers named the “Tall Boys”. These inflatable toys were an immediate sensation, and after the Olympics, Minshall and the engineer filed a patent to begin licensing their design to advertisers. Since then, the inflatable tube dancer has become a great commercial and artistic success, and to this day remains as popular as ever.

A “Tall Boy” at the 1996 Summer Olympics in Atlanta
But how do these inflatable tubes work? To put it succinctly, they work due to Bernoulli’s principle and thin shell buckling. Let me explain. The tube has two holes: one at the bottom where a fan is placed and another at the top (near the hair or fingers). When air is blown into the tube, it travels upwards and creates pressure, pushing the walls of the tube apart and straightening the dancer. Then when the air reaches the top, it is free to escape, causing a rush of air and decrease in pressure inside the tube. This is a direct result of Bernoulli’s principle: an increase in air speed corresponds to a decrease in pressure. So when the pressure decreases, the tube can no longer support its own weight and buckles, causing a kink in the tube (usually near the bottom). When this happens, the mass above the kink falls down, and pressure again builds up inside the tube. The kink is pushed upwards as the pressure builds, until the air escapes again from the top, repeating the cycle. Here’s a nice illustration [1]:
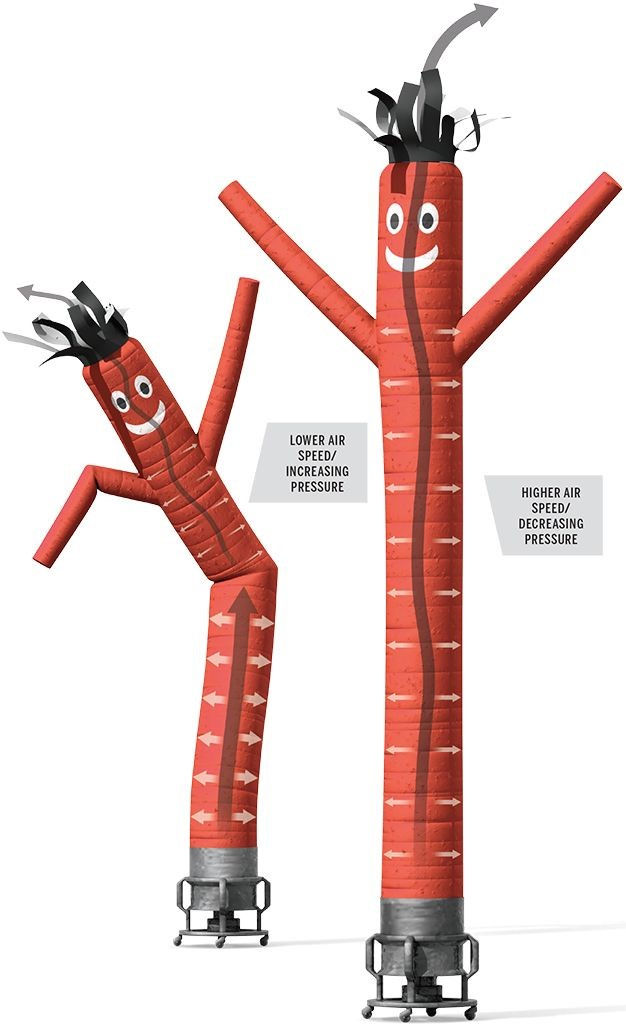
Bernoulli's principle + thin shell buckling
So the design of the inflatable dancer really comes down to choosing the right tube dimensions and fan speed, so that the tube buckles under its own weight when the air escapes at the top. The unpredictability of how the tube buckles is what leads to its “dancing moves”.
What’s wild is that this is a similar problem to what NASA engineers deal with when designing rockets. However, their goal is the reverse: they don’t want the rocket to buckle under its self-weight. And this has always been a challenge, from the early days of NASA to today:

Atlas D-Agena rocket buckling under its self-weight, due to loss of internal pressure, 1963
Today, there are equations and empirical formulas to predict whether a tube will buckle under its self-weight. For example, in the case of a tube under axial compression and internal pressure (i.e. from self-weight and internal air pressure), the following formula gives the critical buckling load [2]:
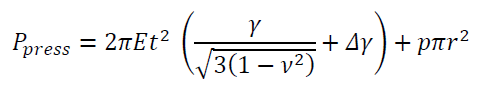
Here the important variables are the properties of the tube material (Young’s modulus E, Poisson ratio v), the dimensions (tube radius r, wall thickness t), and the internal pressure p.
What this equation tells us is that the internal pressure p increases the buckling strength of the tube. And this matches the movement of our inflatable dancer: as the pressure builds inside the tube, it straightens out and can support its own weight. But once the internal pressure decreases, the critical load is less than the self-weight of the tube and it buckles or “dances” as it falls.
Thin shell buckling is a nuanced topic with lots of theory and experiments. People have spent their whole careers thinking about this topic, and there have been many books written on it as well. One key result that NASA discovered early on is that the critical buckling strength predicted by equations like above are mainly theoretical. Even small imperfections in the tube geometry can drastically decrease the critical buckling load. It is also very difficult to exactly predict the tube’s shape after the it buckles. Some tools exist to predict this “post-buckling deformation” as it is called (shameless plug: we do this in my paper), but we can never be sure. And to me, this is what makes the inflatable dancer truly remarkable – we can never be sure just what dance move will be next.
References/further reading:
[1] “How the wacky waving inflatable tube man pulls off those fresh moves,” 2017.
[2] “Buckling of thin-walled circular cylinders,” NASA, 2020.



Comments