How does a pencil break?

Have you ever broken your pencil while writing? Have you ever wondered how and why it breaks?

You might rarely use a wooden pencil in your daily life. Maybe a pen or dry-erase marker is your go-to writing utensil. But the wooden pencil (such as the classic #2) has been an essential writing tool for centuries. Yep, centuries: the history of the modern pencil dates all the way back to 1565, when a large graphite mine was discovered in England [1]. At first the graphite was simply enclosed in a wooden protective case to keep the writer’s hands clean, but soon pencils began to improve and pencil-making became a large business in its own right. Many companies popped up across Europe and the US; even Henry David Thoreau (the guy who wrote Walden) had his own pencil-making company in Massachusetts. Interestingly, these companies were quite secretive about their manufacturing process, especially the ratio of graphite to clay for achieving both a good black mark and a sufficient hardness for the pencil to not break. Hence even today, there are not too many academic papers published on the design of the pencil. Nonetheless you can find some fun pencil ads from the 1900s boasting the unique features of various pencils [2, 3]:

Pencil advertisements from 1950s-1970s

Anyways, the point of this post (pun intended) is to discuss an engineering problem related to the wooden pencil: how exactly does it break when you push it too hard against a writing surface? I came across this question while reading Henry Petroski’s The Pencil, a book which discusses the history of the pencil in an engineering context. This book mentions an article written in 1979 which discusses “broken-off pencil points,” i.e. the pieces of graphite which break off while writing due to excessive pressure. The engineer who wrote this paper observed that all such broken-off pencil points looked the same, no matter the pencil used. Digging a bit deeper, I found various studies which discuss how graphite breaks off a pencil while writing. What’s fascinating is that all the studies use simple concepts from strength of materials to explain the fracture of the graphite. And the simple theory is enough to explain the size of the broken-off pencil points!

The earliest study, writing in 1979 by Cronquist [4], models the tip of a wooden pencil as a conical cantilever beam with a transversely applied load from the writing surface:

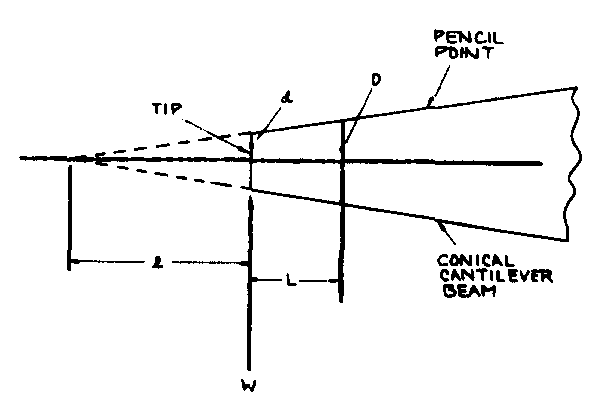
Model of the writing tip of a pencil as a conical cantilever beam

Since pencils cannot be sharpened to a mathematically exact point, the cone is truncated a small distance away from the tip, at the cross-sectional diameter d. Now since graphite is a brittle material, its tensile strength is quite low compared to its compressive strength. Hence the cause of failure is likely the tensile bending stress from the writing load W. For a cantilever beam of length L with constant circular cross section of diameter D, this maximum bending stress is given by:

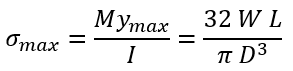
In this case we have a slight taper of the cross section, so we can adjust this equation using the geometry of the taper, i.e. D = (L+l)(d/l), which yields:

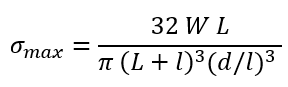
Now to find the location of the maximum tensile stress along the conical beam, we take the derivative of the bending stress w.r.t to the length L and set equal to zero, yielding:

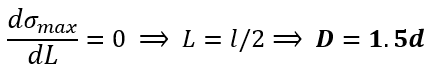
Therefore, the point of maximum tensile stress and hence the most probable location of fracture is when the cross sectional diameter of the graphite is 1.5 times that at the writing tip. This result aligns with our experience: a pencil with a sharp writing tip (small d), will break closer to the tip than a pencil with a dull writing tip (large d). What’s remarkable is that this result is independent of any material properties of the graphite and actually matches well with experiments [5].

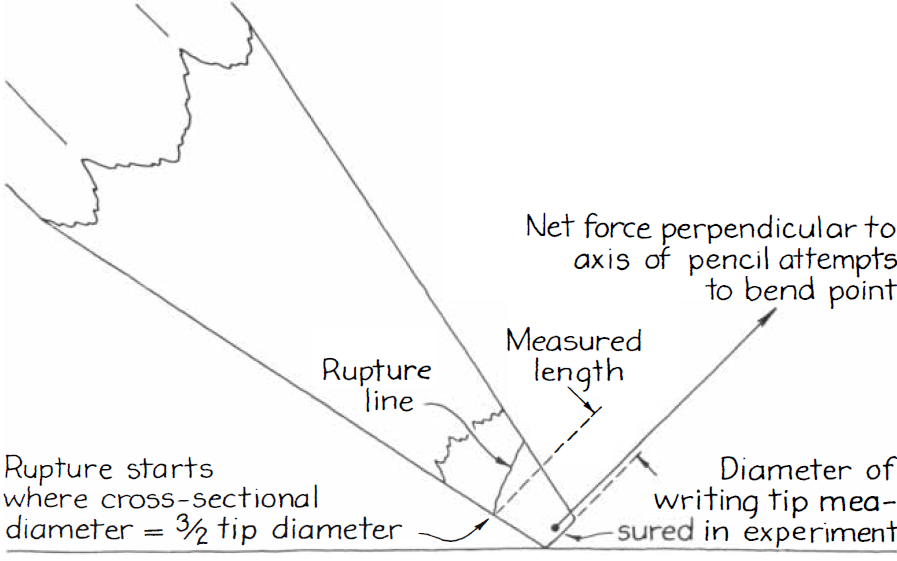
Illustration of a pencil point breaking.

I did some experiments of my own by sharpening and breaking a few pencil points:

For each broken-off pencil point, I found the writing tip diameter was d ≈ 1.3 mm and the diameter at fracture was D ≈ 2 mm, giving a ratio of around 1.53 which matches closely with the above analysis. And all the broken-off pencil points do indeed look similar, as Cronquist observed.

Now this is isn’t the end of the story. Some years later, in 1983 and 1987, two additional papers were published extending this simple model for broken-off pencil points. In the second paper [6], the writing angle of the pencil was included, as well as an axial force along the axis of the pencil and a concentrated bending moment at the writing tip. These additional loads were resolved from the reaction and friction forces on the pencil:

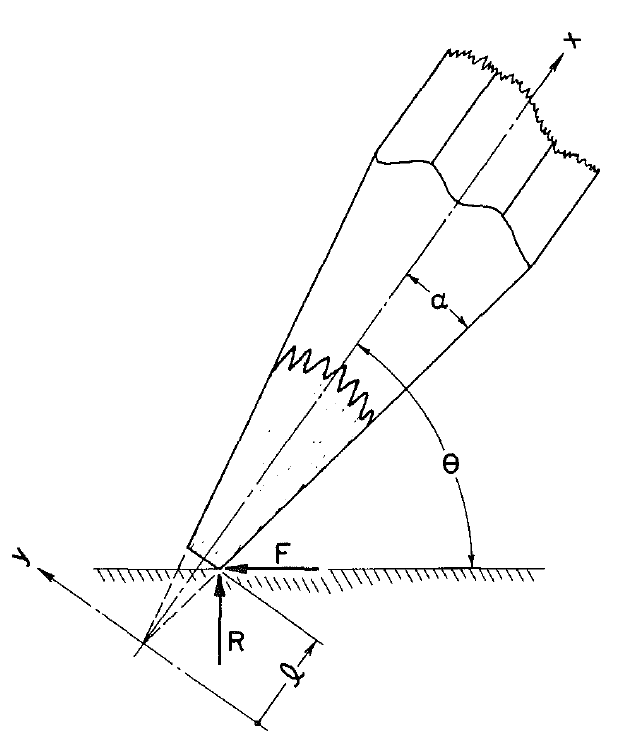
Model of a pencil against a writing surface at an inclined angle.

Using the same analysis of a tapered cantilever beam and the point of maximum tensile stress, an equation was derived for the size of the broken-off pencil point, as a function of the writing angle and taper angle of the pencil (but again independent of any material properties). For a typical writing angle of 45 deg and a taper angle of 6 deg, the ratio of writing tip diameter to slanted length of the broken-off pencil point was calculated to be within 1.46 and 3.32, which indeed matched the experiments in [5].

Pencil with a wedge-shaped writing tip.

And yet a third paper [6] looked at pencils with wedge-shaped writings tips instead of tapered conical tips. This paper used a more advanced linear elasticity solution to calculate the size of broken-off wedges and found that on average, the wedge-shaped point resulted in larger broken-off pieces than the conical point. Since breaking off larger pieces generally requires more energy, this means that breaking wedge-shaped pencils is harder than ones with conical points.

What about for a mechanical lead pencil? There the cross section is not tapered and remains circular along the length of the writing tip. Hence it can be modeled as a cantilever beam with a constant cross section, for which the maximum bending stress is always at the root of the beam, i.e. where the lead exits the pencil. And that’s indeed where it breaks!

To me, all these examples are fascinating applications of the mechanics of materials. They really show the power of simple yet elegant solutions from beam theory. The applications are really all around us!

References/further reading:

[1] The Pencil, Petroski 1990

[2] “Vintage pencil ads,” http://www.pencilrevolution.com/2011/03/excellent-vintage-pencils-ads/

[3] “Vintage Ticonderoga Ads,” https://www.leadfast.org/blog/2018/1/11/tbt-vintage-ticonderoga-ads

[4] “Broken-off pencil points,” Cronquist 1979. https://doi.org/10.1119/1.11954

[5] “The Amateur Scientist: Strange to relate, smokestacks and pencil points break in the same way,” Walker 1979. https://www.jstor.org/stable/24965134

[6] “A note on broken pencil points,” Cowin 1983. https://doi.org/10.1115/1.3167059

[7] “On the fracture of pencil points,” Petroski 1987. https://doi.org/10.1115/1.3173100

[8] "Examiantion of the stress distribution in the tip of a pencil," Pogozelski 2006. https://doi.org/10.1115/1.2062847

[9] "Investigatin of pencil-lead breaks as acoustic emission sources," Sause 2011. https://d-nb.info/1212797574/34